Era of massive data sets brings fascinating problems at the interfaces between information theory and
(statistical) learning theory.
There are various studied connections between information theory and statistics:
- Hypothesis testing, large deviations
- Fisher information, Kullback-Leibler divergence
- Metric entropy and Fano’s inequality
- etc...
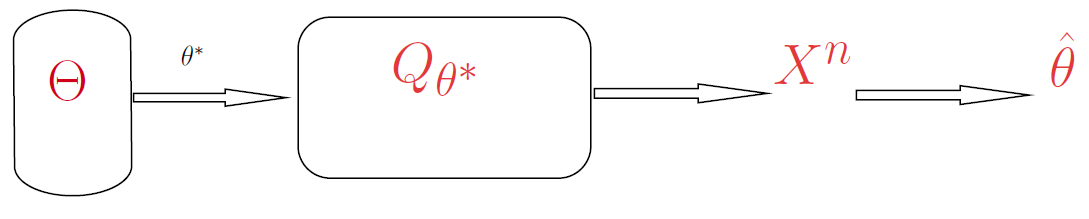
In their classic paper, Kolmogorov and Tikhomirov(1959) make connections between statistical estimation, metric entropy and the notion of channel capacity. Let’s write and draw this in information theoretic jargon. Let;
Codebook: indexed parametric family of probability distributions \(\{Q_\theta | \theta \in
\Theta\}\)
Codeword: nature chooses some parameter \(\theta^\ast \in
\Theta\) (the so-called True Parameter value)
Channel: user observes \(n\) i.i.d. draws from the true distribution \(X_i \sim Q_\theta^\ast\)
Decoding: estimator \(X^n \mapsto \hat{\theta}\) such that \(\hat{\theta}\overset{\mathbb{P}}{\rightarrow}\theta^\ast\)
The setting could be defined in many variations:
| codebooks/codewords: | graphs, vectors, matrices, functions, densities,etc. |
| channels: | random graphs, regression models, elementwise probes of vectors/machines, random projections ,etc. |
| closeness notion: | exact/partial graph recovery in Hamming, \(l^p\) distances, \(L^P\)(Q)-distances, sup-norm etc. |